För det första är den enda säkerheten att det inte finns någon säkerhet. För det andra är varje beslut som en konsekvens en fråga om att väga sannolikheter. För det tredje, trots osäkerhet måste vi bestämma oss och vi måste agera. Och slutligen måste vi bedöma beslut inte bara utifrån resultaten, utan hur dessa beslut fattades. – Robert E. Rubin
En av de viktigaste och mest utmanande aspekterna av prognoser är att hantera den osäkerhet som är inneboende i att granska framtiden. Efter att ha byggt och befolkat hundratals finansiella och operativa modeller för LBO:er, startup-insamlingar, budgetar, M&A och företags strategiska planer sedan 2003, har jag sett ett brett utbud av metoder för att göra det. Varje VD, CFO, styrelseledamot, investerare eller investeringskommittémedlem tar med sin egen erfarenhet och inställning till finansiella prognoser och osäkerhet – påverkad av olika incitament. Ofta ger en jämförelse av faktiska utfall mot prognoser en uppskattning av hur stora avvikelserna mellan prognoser och faktiska utfall kan vara, och därför behovet av att förstå och uttryckligen erkänna osäkerhet.
Jag började till en början använda scenario- och känslighetsanalyser för att modellera osäkerhet, och anser dem fortfarande vara mycket användbara verktyg. Sedan jag lade till Monte Carlo-simuleringar i min verktygslåda 2010 har jag tyckt att de är ett extremt effektivt verktyg för att förfina och förbättra hur du tänker kring risker och sannolikheter. Jag har använt metoden för allt från att konstruera DCF-värderingar, värdera köpoptioner i M&A och diskutera risker med långivare till att söka finansiering och vägleda allokeringen av VC-finansiering för startups. Tillvägagångssättet har alltid mottagits väl av styrelseledamöter, investerare och ledningsgrupper. I den här artikeln ger jag en steg-för-steg handledning om hur du använder Monte Carlo-simuleringar i praktiken genom att bygga en DCF-värderingsmodell.
Innan vi börjar med fallstudien, låt oss gå igenom några olika metoder för att hantera osäkerhet. Begreppet förväntat värde —det sannolikhetsvägda genomsnittet av kassaflöden i alla möjliga scenarier — är Finance 101. Men finansproffs, och beslutsfattare mer allmänt, tar väldigt olika tillvägagångssätt när de omsätter denna enkla insikt i praktiken. Tillvägagångssättet kan sträcka sig från att helt enkelt inte känna igen eller diskutera osäkerhet alls, å ena sidan, till sofistikerade modeller och mjukvara å andra sidan. I vissa fall ägnar människor mer tid åt att diskutera sannolikheter än att beräkna kassaflöden.
Bortsett från att helt enkelt inte ta itu med det, låt oss undersöka några sätt att hantera osäkerhet i prognoser på medellång eller lång sikt. Många av dessa borde vara bekanta för dig.
| Skapar ett scenario. Detta tillvägagångssätt är standard för budgetar, många nystartade företag och till och med investeringsbeslut. Förutom att den inte innehåller någon information om graden av osäkerhet eller insikt om att utfall kan skilja sig från prognoserna, kan den vara tvetydig och tolkas olika beroende på intressent. Vissa kan tolka det som ett sträckmål, där det är mer sannolikt att det faktiska resultatet kommer till kort än överskrider. Vissa ser det som en baslinjeprestanda med mer uppsida än nackdel. Andra kan se det som ett "Base Case" med 50/50 sannolikhet upp och ner. I vissa tillvägagångssätt, särskilt för nystartade företag, är det mycket ambitiöst och misslyckande eller underskott är det mest troliga resultatet, men en högre diskonteringsränta används i ett försök att ta hänsyn till risken. | 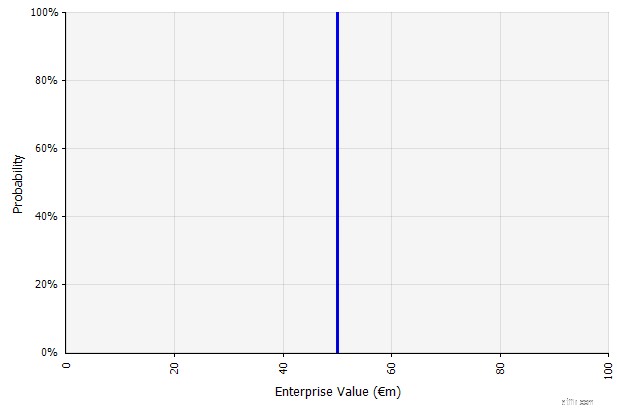 Indata i den långsiktiga kassaflödesprognosen under detta tillvägagångssätt är alla punktskattningar, vilket ger ett punktskattningsresultat på 50 miljoner euro i detta exempel, med en implicit sannolikhet på 100 %. |
| Skapa flera scenarier. Detta tillvägagångssätt inser att verkligheten sannolikt inte kommer att utvecklas enligt en enda given plan.
| 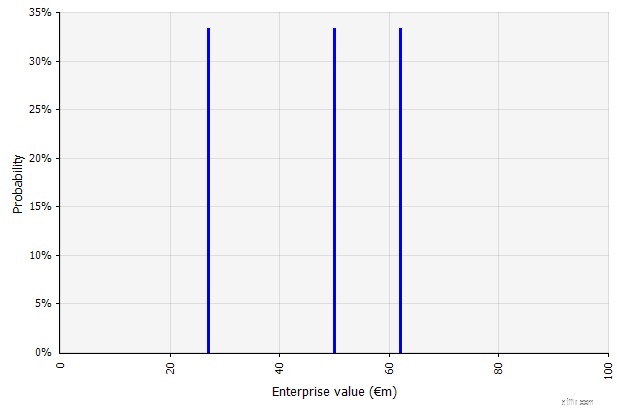 De tre olika scenarierna ger tre olika resultat, här antas vara lika sannolika. Sannolikheterna för utfall utanför de höga och låga scenarierna beaktas inte. |
| Skapa bas-, upp- och nedåtfall med sannolikheter som uttryckligen identifieras. Det vill säga att björn- och tjurfallen innehåller till exempel 25 % sannolikhet i varje svans, och uppskattningen av verkligt värde representerar mittpunkten. En användbar fördel med detta ur ett riskhanteringsperspektiv är den explicita analysen av svansrisk, d.v.s. händelser utanför upp- och nedsidans scenarier. | Illustration från Morningstar Valuation Handbook 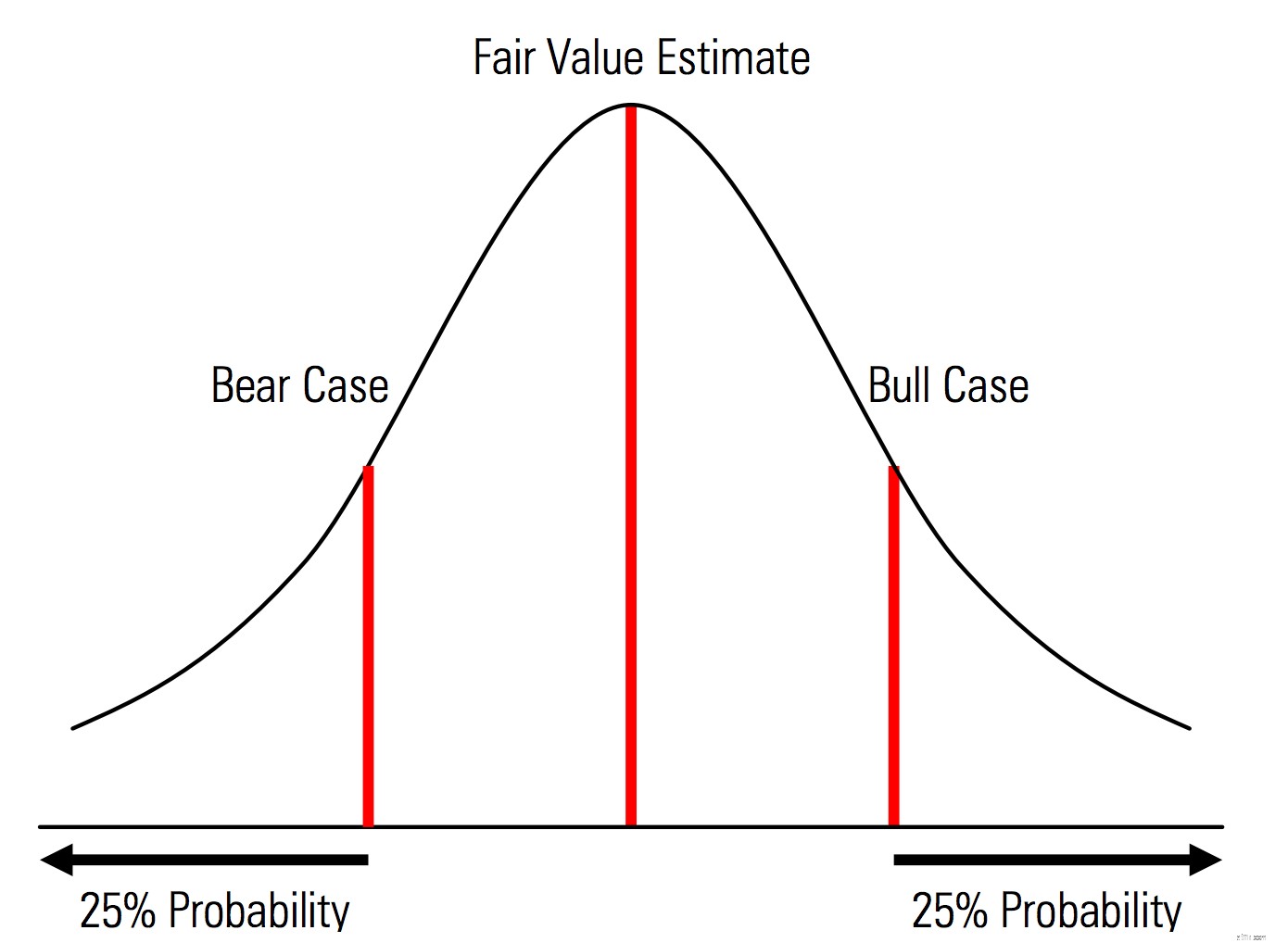 |
| Använda sannolikhetsfördelningar och Monte Carlo-simuleringar. Genom att använda sannolikhetsfördelningar kan du modellera och visualisera hela skalan av möjliga utfall i prognosen. Detta kan göras inte bara på en aggregerad nivå, utan också för detaljerade individuella input, antaganden och drivkrafter. Monte Carlo-metoder används sedan för att beräkna de resulterande sannolikhetsfördelningarna på en aggregerad nivå, vilket möjliggör analys av hur flera osäkra variabler bidrar till osäkerheten i de övergripande resultaten. Kanske viktigast av allt, tillvägagångssättet tvingar alla inblandade i analysen och beslutet att uttryckligen inse osäkerheten som är inneboende i prognoser och att tänka i sannolikheter. Precis som de andra tillvägagångssätten har detta sina nackdelar, inklusive risken för falsk precision och resulterande övertro som kan komma med att använda en mer sofistikerad modell, och det extra arbete som krävs för att välja lämpliga sannolikhetsfördelningar och uppskatta deras parametrar där annars endast punktskattningar skulle vara används. | 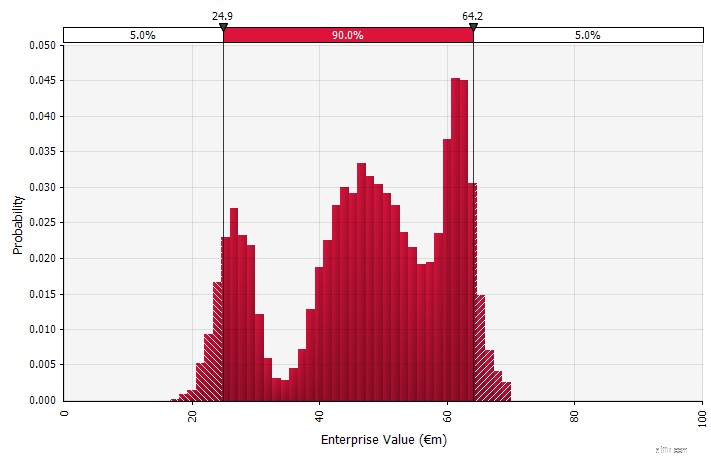 |
Monte Carlo-simuleringar modellerar sannolikheten för olika utfall i finansiella prognoser och uppskattningar. De får sitt namn från området Monte Carlo i Monaco, som är världsberömt för sina exklusiva kasinon; slumpmässiga utfall är centrala för tekniken, precis som de är för roulette och spelautomater. Monte Carlo-simuleringar är användbara inom ett brett spektrum av områden, inklusive teknik, projektledning, olje- och gasprospektering och andra kapitalintensiva industrier, FoU och försäkring; här fokuserar jag på tillämpningar inom finans och affärer.
I simuleringen beskrivs de osäkra ingångarna med hjälp av sannolikhetsfördelningar, beskrivna med parametrar som medelvärde och standardavvikelse. Exempel på indata i finansiella prognoser kan vara allt från intäkter och marginaler till något mer detaljerat, som råvarupriser, investeringar för en expansion eller utländska växelkurser.
När en eller flera indata beskrivs som sannolikhetsfördelningar blir utdata också en sannolikhetsfördelning. En dator drar slumpmässigt ett tal från varje ingångsfördelning och beräknar och sparar resultatet. Detta upprepas hundratals, tusentals eller tiotusentals gånger, var och en kallas en iteration. Tillsammans approximerar dessa iterationer sannolikhetsfördelningen för det slutliga resultatet.
Ingångsfördelningarna kan antingen vara kontinuerliga , där det slumpmässigt genererade värdet kan ta vilket värde som helst under fördelningen (till exempel en normalfördelning), eller diskret , där sannolikheter är kopplade till två eller flera distinkta scenarier.
En simulering kan också innehålla en blandning av distributioner av olika typer. Ta till exempel ett farmaceutiskt FoU-projekt med flera stadier som var och en har en diskret sannolikhet för framgång eller misslyckande. Detta kan kombineras med kontinuerliga distributioner som beskriver osäkra investeringsbelopp som behövs för varje steg och potentiella intäkter om projektet resulterar i en produkt som når marknaden. Diagrammet nedan visar resultatet från en sådan simulering:en ~65 % sannolikhet att förlora hela investeringen på 5 miljoner euro till 50 miljoner euro (nuvärde), och en ~35 % sannolikhet för en nettovinst troligen i intervallet 100 € till 250 € – information som skulle gå förlorad om viktiga utdatamått som MIRR eller NPV visas som punktuppskattningar snarare än sannolikhetsfördelningar.
Exempel Monte Carlo-simulering för ett projekt med flera Go/No-go-stadier och osäkra investeringar däremellan, med osäkert värde om projektet når slutförande
En anledning till att Monte Carlo-simuleringar inte används mer allmänt är att typiska dagliga finansverktyg inte stöder dem särskilt bra. Excel och Google Sheets innehåller ett tal eller formelresultat i varje cell, och även om de kan definiera sannolikhetsfördelningar och generera slumpmässiga tal är det krångligt att bygga en finansiell modell med Monte Carlo-funktionalitet från början. Och medan många finansinstitut och värdepappersföretag använder Monte Carlo-simuleringar för att värdera derivat, analysera portföljer och mer, är deras verktyg vanligtvis utvecklade internt, proprietära eller oöverkomligt dyra – vilket gör dem otillgängliga för den enskilde finanspersonalen.
Därför vill jag uppmärksamma Excel-plugins som @RISK by Palisade, ModelRisk by Vose och RiskAMP, som avsevärt förenklar arbetet med Monte Carlo-simuleringar och låter dig integrera dem i dina befintliga modeller. I följande genomgång kommer jag att använda @RISK.
Låt oss gå igenom ett enkelt exempel som illustrerar nyckelbegreppen i en Monte Carlo-simulering:en femårig kassaflödesprognos. I den här genomgången ställer jag upp och fyller i en grundläggande kassaflödesmodell för värderingsändamål, ersätter gradvis indata med sannolikhetsfördelningar och kör slutligen simuleringen och analyserar resultaten.
Till att börja med använder jag en enkel modell, fokuserad på att lyfta fram nyckelfunktionerna i att använda sannolikhetsfördelningar. Observera att till att börja med skiljer sig denna modell inte från någon annan Excel-modell; plugin-programmen jag nämnde ovan fungerar med dina befintliga modeller och kalkylblad. Modellen nedan är en enkel hyllversion fylld med antaganden för att bilda ett scenario.
Först måste vi samla in den information som behövs för att göra våra antaganden, sedan måste vi välja rätt sannolikhetsfördelningar att infoga. Det är viktigt att notera att källan till de viktigaste indata/antagandena är desamma oavsett vilket tillvägagångssätt du tar för att hantera osäkerhet. Kommersiell due diligence, en omfattande genomgång av företagets affärsplan mot bakgrund av förväntad marknadsutveckling, branschtrender och konkurrensdynamik, inkluderar vanligtvis extrapolering från historiska data, inkorporering av expertutlåtanden, genomför marknadsundersökningar och intervjuer marknadsdeltagare. Enligt min erfarenhet diskuterar experter och marknadsaktörer gärna olika scenarier, risker och olika resultat. De flesta beskriver dock inte explicit sannolikhetsfördelningar.
Låt oss nu gå igenom och ersätta våra viktigaste ingångsvärden med sannolikhetsfördelningar en efter en, med början på den beräknade försäljningstillväxten för det första prognosåret (2018). @RISK-plugin för Excel kan utvärderas med en 15-dagars gratis provperiod så att du kan ladda ner den från Palisade-webbplatsen och installera den med några få klick. Med @RISK-pluginen aktiverad, välj den cell du vill ha distributionen i och välj "Definiera distribution" i menyn.
Du väljer sedan en från paletten av distributioner som kommer upp. Mjukvaran @RISK erbjuder mer än 70 olika distributioner att välja mellan, så att välja en kan verka överväldigande till en början. Nedan följer en guide till en handfull jag använder oftast:
| Normal. Definieras av medelvärde och standardavvikelse. Detta är en bra utgångspunkt på grund av dess enkelhet och lämplig som en förlängning av Morningstar-metoden, där du definierar en fördelning som täcker kanske redan definierade scenarier eller intervall för en given ingång, vilket säkerställer att fallen är symmetriska runt basfallet och att sannolikheterna i varje svans ser rimliga ut (säg 25 % som i Morningstar-exemplet). | 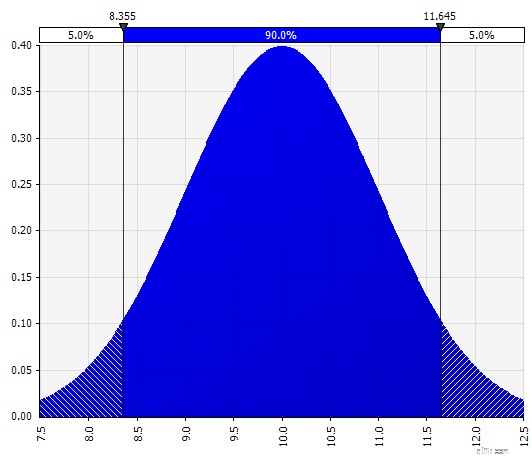 |
| Johnson Moments. Genom att välja detta kan du definiera snedfördelningar och fördelningar med fetare eller tunnare svansar (tekniskt lägga till parametrar för skevhet och kurtos). Bakom kulisserna använder detta en algoritm för att välja en av fyra distributioner som återspeglar de fyra valda parametrarna, men det är osynligt för användaren --- allt vi behöver fokusera på är parametrarna.
| 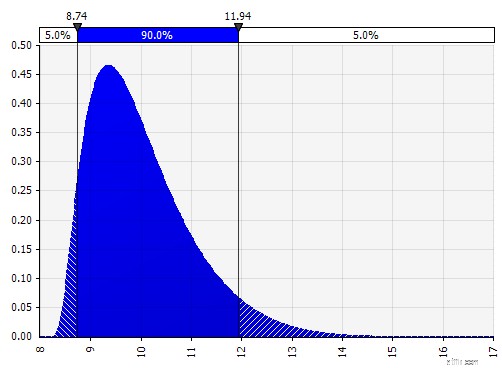 |
| Diskret. Där sannolikheter ges till två eller flera specifika värden. För att återgå till exemplet med stegvis FoU-projekt i början, modelleras sannolikheten för framgång i varje steg som en binär diskret fördelning, med ett utfall på 1 som representerar framgång och 0 misslyckande. | 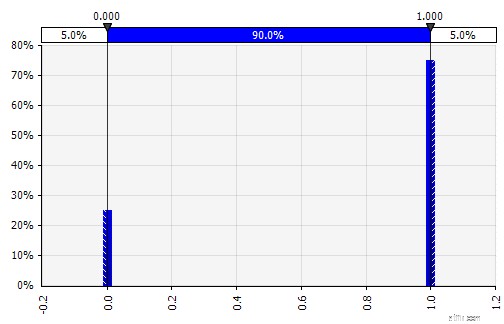 |
| Distributionsanpassning. När du har en stor mängd historiska datapunkter är distributionsanpassningsfunktionen användbar. Det betyder till exempel inte tre eller fyra år av historisk försäljningstillväxt, utan tidsseriedata som råvarupriser, valutakurser eller andra marknadspriser där historien kan ge användbar information om framtida trender och graden av osäkerhet. | 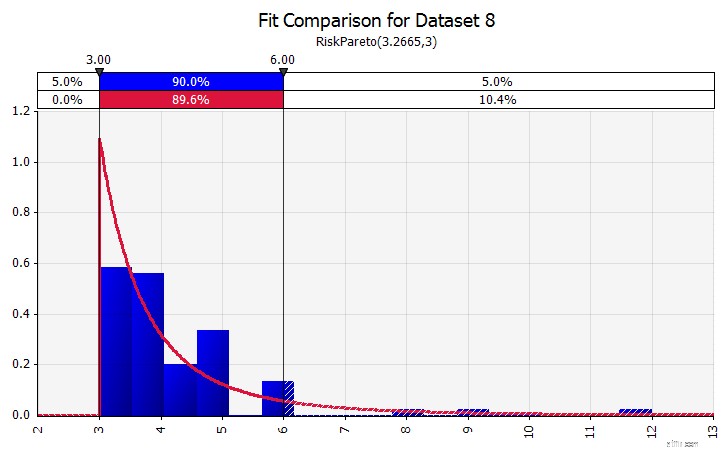 |
| Kombinera flera olika distributioner till en. För att mildra den potentiella effekten av individuella fördomar är det ofta en bra idé att inkludera input från olika källor i ett antagande och/eller att granska och diskutera resultaten. Det finns olika tillvägagångssätt:
| 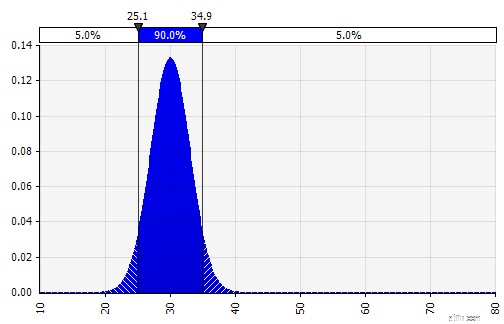 Vikt:20 % 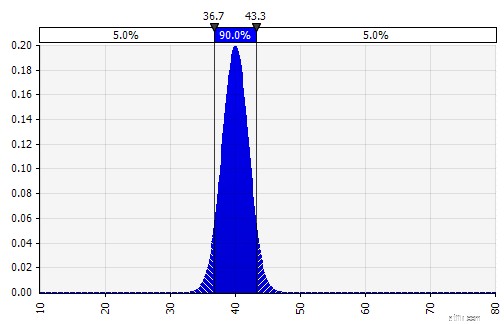 Vikt:20 % 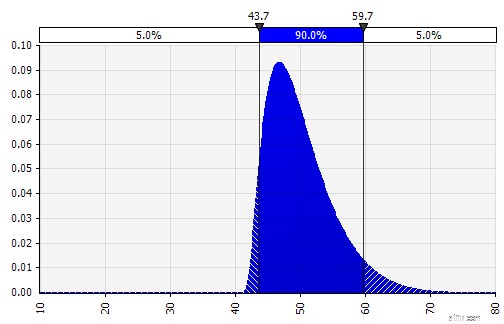 Vikt:60 % 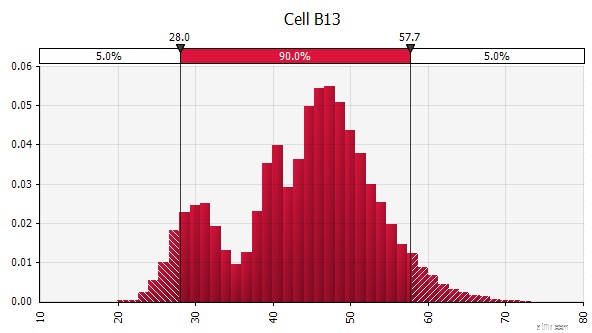 |
| Frihand. För att snabbt illustrera en distribution som en del av diskussioner eller om du behöver en distribution när du ritar en modell som inte är lätt att skapa från den befintliga paletten, är frihandsfunktionen användbar. Som namnet antyder låter detta dig rita fördelningen med ett enkelt målningsverktyg. | 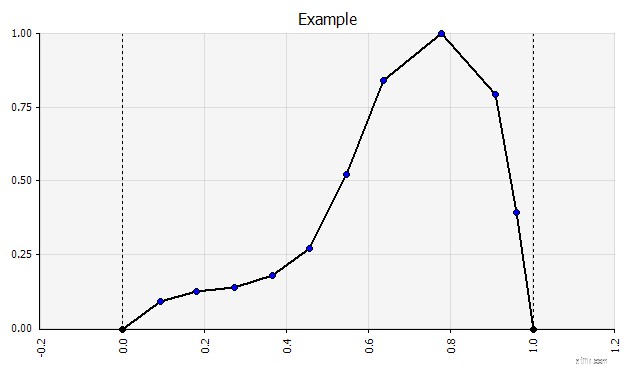 |
Nu ser vi en visualisering av fördelningen, med några parametrar på vänster sida. Symbolerna för medelvärde och standardavvikelse bör se bekanta ut. I fallet med en normalfördelning skulle medelvärdet vara det vi tidigare angav som ett enskilt värde i cellen. Här är sannolikhetsfördelningen för 2018 som ett exempel, där 10 % representerar medelvärdet. Medan din typiska modell antingen bara fokuserar på siffran på 10 % eller har scenarier för "tjur" och "björn" med kanske 15 % respektive 5 % tillväxt, ger denna nu information om hela spektrumet av förväntade potentiella utfall.
Sannolikhetsfördelning av försäljningstillväxt på ett år
En fördel med Monte Carlo-simuleringar är att svansresultat med låg sannolikhet kan utlösa tänkande och diskussioner. Att endast visa upp- och nedåtscenarier kan introducera risken att beslutsfattare tolkar dessa som de yttre gränserna och avfärdar alla scenarier som ligger utanför. Detta kan resultera i felaktigt beslutsfattande, med exponering för resultat som ligger utanför organisationens eller individens risktolerans. Även en sannolikhet på 5 % eller 1 % kan vara oacceptabel om scenariot i fråga skulle få katastrofala konsekvenser.
Med Monte Carlo-modellering, var uppmärksam på hur osäkerhets- och sannolikhetsfördelningar staplas ovanpå varandra, till exempel över tid. Låt oss granska ett exempel. Eftersom försäljningen varje år beror på tillväxten under de föregående, kan vi visualisera och se att vår uppskattning av försäljningen för 2022 är mer osäker än den för 2018 (visas med standardavvikelser och 95 % konfidensintervall varje år). För enkelhetens skull specificerar exemplet nedan tillväxten för ett år, 2018, och tillämpar sedan samma tillväxttakt för vart och ett av följande år fram till 2022. Ett annat tillvägagångssätt är att ha fem oberoende fördelningar, en för varje år.
Illustrerar hur osäkerheten ökar med tiden (vidgare fördelningen av resultat)
Vi uppskattar nu en sannolikhetsfördelning för EBIT-marginalen 2018 (markerad nedan) på samma sätt som vi gjorde det för försäljningstillväxt.
Här kan vi använda korrelationsfunktionen för att simulera en situation där det finns en tydlig korrelation mellan relativ marknadsandel och lönsamhet, vilket återspeglar stordriftsfördelar. Scenarier med högre försäljningstillväxt i förhållande till marknaden och motsvarande högre relativ marknadsandel kan modelleras ha en positiv korrelation med högre EBIT-marginaler. I branscher där ett företags förmögenhet är starkt korrelerad med någon annan extern faktor, såsom oljepriser eller valutakurser, kan det vara meningsfullt att definiera en fördelning för den faktorn och modellera en korrelation med försäljning och lönsamhet.
Modellering av korrelation mellan försäljningstillväxt och marginaler
Beroende på tillgänglig tid, transaktionsstorlek och andra faktorer är det ofta meningsfullt att bygga en operativ modell och mata in de mest osäkra variablerna explicit. Dessa inkluderar:produktvolymer och priser, råvarupriser, valutakurser, viktiga omkostnader, aktiva användare varje månad och genomsnittlig intäkt per enhet (ARPU). Det är också möjligt att modellera bortom mängdvariabler som utvecklingstid, tid till marknad eller marknadsanpassningshastighet.
Med det skisserade tillvägagångssättet kan vi nu fortsätta genom balansräkningen och kassaflödesanalysen, fylla med antaganden och använda sannolikhetsfördelningar där det är meningsfullt.
En notering om capex:detta kan modelleras antingen i absoluta belopp eller som en procentandel av försäljningen, eventuellt i kombination med större stegvisa investeringar; en tillverkningsanläggning kan till exempel ha en tydlig kapacitetsgräns och en stor expansionsinvestering eller en ny anläggning nödvändig när försäljningen överstiger tröskeln. Eftersom var och en av de säg 1 000 eller 10 000 iterationerna kommer att vara en fullständig omräkning av modellen, kan en enkel formel som utlöser investeringskostnaden om/när en viss volym uppnås användas.
Att bygga en Monte Carlo-modell har ytterligare ett steg jämfört med en vanlig finansiell modell:De celler där vi vill utvärdera resultaten måste specifikt betecknas som utdataceller. Programvaran kommer att spara resultaten av varje iteration av simuleringen för dessa celler för oss att utvärdera efter att simuleringen är klar. Alla celler i hela modellen räknas om med varje iteration, men resultaten av iterationerna i andra celler, som inte är betecknade som in- eller utdataceller, går förlorade och kan inte analyseras efter att simuleringen är klar. Som du kan se i skärmdumpen nedan utser vi MIRR-resultatcellen till en utdatacell.
När du har byggt färdigt modellen är det dags att köra simuleringen för första gången genom att helt enkelt trycka på "start simulering" och vänta i några sekunder.
Utdata uttryckt som sannolikheter. Medan vår modell tidigare gav oss ett enda värde för den modifierade IRR, kan vi nu tydligt se att det finns ett antal potentiella utfall runt det värdet, med olika sannolikheter. Detta gör det möjligt för oss att omformulera frågor, som "Kommer vi att nå vår avkastningsgrad med den här investeringen?" till "Hur sannolikt är det att vi når eller överskrider vår hinderfrekvens?" Du kan utforska vilka utfall som är mest sannolikt med hjälp av till exempel ett konfidensintervall. Visualiseringen är användbar när du kommunicerar resultaten till olika intressenter, och du kan lägga över utdata från andra transaktioner för att visuellt jämföra hur attraktiv och (o)säker den nuvarande är jämfört med andra (se nedan).
Modifierad IRR med konfidensintervall
Modifierad IRR med en hinderfrekvens
Modifierad IRR med andra transaktioner överlagrade
Förstå graden av osäkerhet i slutresultatet. Om vi genererar ett diagram över kassaflödesvariabilitet över tid, liknande det vi gjorde initialt för försäljning, blir det tydligt att variationen i fritt kassaflöde blir betydande även med relativt blygsam osäkerhet i försäljningen och de andra indata som vi modellerade som sannolikhetsfördelningar , med resultat som sträcker sig från cirka 0,5 miljoner euro till 5,0 miljoner euro – en faktor på 10x – till och med bara en standardavvikelse från medelvärdet. Detta är resultatet av att osäkra antaganden staplas ovanpå varandra, en effekt som förvärras både "vertikalt" över åren och "horisontellt" ner genom de finansiella rapporterna. Visualiseringarna ger information om båda typerna av osäkerhet.
Variation av fritt kassaflöde jämfört med variation i försäljning
Känslighetsanalys:Introduktion av tornadografen. Ett annat viktigt område är att förstå vilka insatser som har störst inverkan på ditt slutresultat. Ett klassiskt exempel är hur betydelsen av diskonteringsränta eller terminalvärdesantaganden ofta tillmäts för liten vikt i förhållande till kassaflödesprognoser. Ett vanligt sätt att hantera detta är att använda matriser där du lägger en nyckelinmatning på varje axel och sedan beräknar resultatet i varje cell (se nedan). This is useful especially in situations where decisions hinge on one or a few key assumptions—in these “what you have to be believe” situations, decision-makers on (for example) an investment committee or a senior management team may have different views of those key assumptions, and a matrix such as the one above allows each one of them to find a result value corresponding to their view, and can decide, vote, or give advice based on that.
Example Sensitivity Analysis Matrix - Enterprise Value as a Function of the Cost of Capital and Year Five Exit Multiple
Enhancing with Monte Carlo simulations. When using Monte Carlo simulations, that approach can be complemented with another:the tornado diagram. This visualization lists the different uncertain inputs and assumptions on the vertical axis and then shows how large the impact of each is on the end result.
Tornado Diagram Showing Sensitivity to Key Inputs
This has several uses, one of which is that it allows those preparing the analysis to ensure that they are spending time and effort on understanding and validating the assumptions roughly corresponding to how important each is for the end result. It can also guide the creation of a sensitivity analysis matrix by highlighting which assumptions really are key.
Another potential use case is to allocate engineering hours, funds, or other scarce resources to validating and narrowing the probability distributions of the most important assumptions. An example of this in practice was a VC-backed cleantech startup where I used this method to support decision-making both to allocate resources and to validate the commercial viability of its technology and business model, making sure you solve the most important problems, and gather the most important information first. Update the model, move the mean values, and adjust the probability distributions, and continually reassess if you are focused on solving the right problems.
Probability is not a mere computation of odds on the dice or more complicated variants; it is the acceptance of the lack of certainty in our knowledge and the development of methods for dealing with our ignorance. – Nassim Nicholas Taleb
It is useful to distinguish between risk , defined as situations with future outcomes that are unknown but where we can calculate their probabilities (think roulette), and uncertainty , where we cannot estimate the probabilities of events with any degree of certainty.
In business and finance, most situations facing us in practice will lie somewhere in between those two. The closer we are to the risk end of that spectrum, the more confident we can be that when using probability distributions to model possible future outcomes, as we do in Monte Carlo simulations, those will accurately capture the situation facing us.
The closer we get to the uncertainty end of the spectrum, the more challenging or even dangerous it can be to use Monte Carlo simulations (or any quantitative approach). The concept of “fat tails,” where a probability distribution may be useful but the one used has the wrong parameters, has received lots of attention in finance, and there are situations where even the near-term future is so uncertain that any attempt to capture it in a probability distribution at all will be more misleading than helpful.
In addition to keeping the above in mind, is also important to 1) be mindful of the shortcomings of your models, 2) be vigilant against overconfidence, which can be amplified by more sophisticated tools, and 3) bear in mind the risk of significant events that may lie outside what has been seen before or the consensus view.
There are two concepts here and it is important to separate them:one is the recognition of uncertainty and the mindset of thinking in probabilities, and the other is one practical tool to support that thinking and have constructive conversations about it:Monte Carlo simulations in spreadsheets.
I don’t use Monte Carlo simulations in all models I build or work on today, or even a majority. But the work I have done with it influences how I think about forecasting and modeling. Just doing this type of exercise a few times, or even once, can influence how you view and make decisions. As with any model we use, this method remains a gross simplification of a complex world, and forecasters in economics, business, and finance have a disappointing track record when evaluated objectively.
Our models are far from perfect but, over years and decades, and millions or billions of dollars/euros invested or otherwise allocated, even a small improvement in your decision-making mindset and processes can add significant value.
I spend 98% of my time on 2% probabilities – Lloyd Blankfein
Hur man utför plikterna som exekutor för en dödsbo
Varför jag hatar Monte Carlo-analys och andra finansiella prognoser
Satsa inte på din pension på Monte Carlo-modeller
Vad är kvalitativ analys av aktier? Och hur gör man det?
Förklarat:Hur är PESTLE-analys (med exempel)? Hur gör man det?
DMart affärsmodell och framgångsmantra – hur tjänar DMart pengar?
Vad är Portfolio Backtesting? Hur gör man det på indiska aktier?
Hur värderar man aktier med Gordon Growth Model?